Unelastische Reaktion
Die obige Art, [σ] in Bezug auf [S] auszudrücken, gilt auch für Feststoffe, die eine viskoelastische oder plastische Reaktion zeigen, mit der Ausnahme, dass [S] dann nicht nur als Funktion des vorliegenden [E M] anzusehen ist] und θ, aber auch abhängig von der Vorgeschichte beider. Unter der Annahme, dass solche Materialien eine elastische Reaktion auf plötzliche Spannungsänderungen oder auf eine geringe Entlastung aus einem plastisch verformenden Zustand zeigen, kann [S] wie oben immer noch als Ableitung von f ausgedrückt werden, aber die Ableitung wird als in Bezug auf eine Elastizität genommen verstanden Variation der Dehnung und ist bei festem θ und mit fester vorheriger unelastischer Verformung und Temperaturhistorie zu nehmen. Eine solche Abhängigkeit von der Geschichte wird manchmal als Abhängigkeit von f von internen Zustandsvariablen dargestellt, deren Evolutionsgesetze Teil der unelastischen konstitutiven Beschreibung sind. Es gibt auch einfachere Modelle der unelastischen Reaktion, und die am häufigsten verwendeten Formen für Plastizität und Kriechen in isotropen Festkörpern werden als nächstes vorgestellt.
In guter Näherung bewirkt die plastische Verformung kristalliner Feststoffe keine Volumenänderung; und hydrostatische Spannungsänderungen, die einer gleichen Änderung aller normalen Spannungen entsprechen, haben keinen Einfluss auf den plastischen Fluss, zumindest bei Änderungen, die in der gleichen Größenordnung oder Größenordnung wie die Festigkeit des Feststoffs bei Scherung liegen. Daher wird die plastische Antwort normalerweise als deviatorische Spannung formuliert, die durch τ ij = σ ij - δ ij (σ 11 + σ 22 + σ 33) / 3 definiert ist. In Anlehnung an Richard von Mises wird in einem Verfahren, das mit dem Experiment mäßig gut übereinstimmt, die plastische Fließbeziehung als zweite Invariante der deviatorischen Spannung formuliert, die üblicherweise als umgeschrieben wird
und die äquivalente Zugspannung genannt. Die Definition erfolgt so, dass für einen einachsigen Spannungszustand σ gleich der Zugspannung ist und die Spannungs-Dehnungs-Beziehung für allgemeine Spannungszustände anhand von Daten aus dem Zugversuch formuliert wird. Insbesondere wird eine plastische Dehnung & epsi; p in einem einachsigen Spannungstest aus & epsi; p = & epsi; - & sgr; / E definiert, wobei & epsi; als die Dehnung im Zugversuch gemäß der logarithmischen Definition & epsi; = ln & lgr; interpretiert wird, der Elastizitätsmodul E ist angenommen, dass es bei Verformung unverändert bleibt, und σ / E << 1.
Daher wird in der geschwindigkeitsunabhängigen Plastizitätsversion der Theorie angenommen, dass Zugdaten (oder Druckdaten mit geeigneten Vorzeichenumkehrungen) aus einem monotonen Belastungstest eine Funktion ε p (σ) definieren. In den viskoplastischen oder Hochtemperatur-Kriechversionen der Theorie werden Zugdaten interpretiert, um d & egr; P / dt als Funktion von & sgr; im einfachsten Fall zu definieren, der beispielsweise sekundäres Kriechen darstellt, und als Funktion von & sgr; und & egr; p in Theorien soll vorübergehende Kriecheffekte oder geschwindigkeitsabhängige Reaktionen bei niedrigeren Temperaturen darstellen. Betrachten Sie zunächst das Modell aus starrem Kunststoff, bei dem die elastische Verformbarkeit völlig ignoriert wird, wie es manchmal bei Problemen mit großem plastischem Fluss, bei der Metallumformung oder beim Langzeitkriechen im Erdmantel oder bei der Analyse von plastischen Kollapslasten auf Strukturen angemessen ist. Die Geschwindigkeit des Verformungstensors D ij ist definiert durch 2D ij = ∂v i / ∂x j + ∂v j / ∂x i, und im starrplastischen Fall kann [D] mit dem gleichgesetzt werden, was als sein plastischer Teil angesehen werden kann [D p], gegeben als D p / ij = 3 (d & epsi; p / dt) & tgr; ij / 2 & sgr;. Die numerischen Faktoren sichern die Übereinstimmung zwischen D p / 11 und d & epsi; p / dt für die einachsige Spannung in der 1-Richtung. Die Gleichung impliziert dies auch
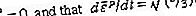
die über die Vorgeschichte integriert werden muss, um ε p zu erhalten, wie es für viskoplastische Modelle erforderlich ist, bei denen dε p / dt eine Funktion von σ und ε p ist. In der ratenunabhängigen Version wird [D p] als Null definiert, wenn σ kleiner als der höchste Wert ist, den es in der Vorgeschichte erreicht hat, oder wenn der aktuelle Wert von σ der höchste Wert ist, aber dσ / dt <0. (Im elastisch-plastischen Kontext bedeutet dies, dass das „Entladen“ nur eine elastische Reaktion beinhaltet.) Für den ideal plastischen Feststoff, der idealisiert ist, um ohne Spannungserhöhung fließen zu können, wenn σ gleich dem Streckgrenze ist, ist dε p / dt wird als unbestimmter, aber notwendigerweise nicht negativer Parameter angesehen, der (manchmal nicht eindeutig) nur durch die vollständige Lösung eines soliden mechanischen Grenzwertproblems bestimmt werden kann.
Das elastisch-plastische Materialmodell wird dann formuliert, indem D ij = D e / ij + D p / ij geschrieben wird, wobei D p / ij in Bezug auf die Spannung und möglicherweise die Spannungsrate wie oben angegeben ist und wo die elastischen Verformungsraten [D e] beziehen sich auf Spannungen durch den üblichen linearen elastischen Ausdruck D e / ij = (1 + ν) σ ij * / E - νδ ij (σ 11 * + σ 22 * + σ 33 *) / E. Hier werden die Spannungsraten als Jaumann-Co-Rotationsraten ausgedrückt

ist eine Ableitung, die der Bewegung eines Materialpunkts folgt und bei der der Spin Ω ij durch 2Ω ij = ∂v i / ∂x j - ∂v j / ∂x i definiert ist. Die Co-Rotationsspannungsraten sind diejenigen, die von einem Beobachter berechnet werden, der sich mit der durchschnittlichen Winkelgeschwindigkeit eines Materialelements dreht. Der elastische Teil der Spannungs-Dehnungs-Beziehung sollte mit der Existenz einer freien Energie f übereinstimmen, wie oben diskutiert. Dies wird durch die gerade gegebene Form nicht unbedingt erfüllt, aber die Unterschiede zwischen ihr und einer auf diese Weise konsistenten Form beinhalten zusätzliche Terme, die in der Größenordnung von σ / E 2 mal dem σ kl * liegen und in typischen Fällen vernachlässigbar sind, in denen Die Theorie wird verwendet, da σ / E normalerweise ein extrem kleiner Bruchteil der Einheit ist, beispielsweise 10 -4 bis 10 -2. Eine Version der Theorie mit geringer Dehnung wird üblicherweise für Zwecke der elastisch-plastischen Spannungsanalyse verwendet. In diesen Fällen wird [D] durch ∂ [ε (X, t)] / ∂t ersetzt, wobei [ε] der Tensor mit geringer Dehnung ist, ∂ / ∂x mit ∂ / ∂X in allen Gleichungen und [σ *] mit ∂ [σ (X, t)] / ∂t. Die letzten beiden Schritte können nicht immer gerechtfertigt werden, selbst bei sehr geringer Dehnung, wenn beispielsweise in einem geschwindigkeitsunabhängigen Material dσ / dε p im Vergleich zu σ nicht groß ist oder wenn die Rotationsgeschwindigkeiten von Materialfasern viel größer werden können als Dehnungsraten, die selbst bei rein elastischen Feststoffen ein Problem für Knickprobleme darstellen.