Differentialgleichung, mathematische Aussage, die eine oder mehrere Ableitungen enthält, dh Begriffe, die die Änderungsraten kontinuierlich variierender Größen darstellen. Differentialgleichungen sind in Wissenschaft und Technik sowie in vielen anderen Bereichen der quantitativen Untersuchung sehr verbreitet, da für Systeme, die Änderungen unterliegen, ihre Änderungsraten direkt beobachtet und gemessen werden können. Die Lösung einer Differentialgleichung ist im Allgemeinen eine Gleichung, die die funktionale Abhängigkeit einer Variablen von einer oder mehreren anderen ausdrückt; Es enthält normalerweise konstante Terme, die in der ursprünglichen Differentialgleichung nicht vorhanden sind. Eine andere Möglichkeit, dies zu sagen, besteht darin, dass die Lösung einer Differentialgleichung eine Funktion erzeugt, mit der das Verhalten des ursprünglichen Systems zumindest innerhalb bestimmter Einschränkungen vorhergesagt werden kann.

Analyse: Newton- und Differentialgleichungen
Die Anwendung der Analyse sind Differentialgleichungen, die die Änderungsraten verschiedener Größen mit ihren aktuellen Werten in Beziehung setzen.
Differentialgleichungen werden in mehrere breite Kategorien eingeteilt, die wiederum weiter in viele Unterkategorien unterteilt werden. Die wichtigsten Kategorien sind gewöhnliche Differentialgleichungen und partielle Differentialgleichungen. Wenn die an der Gleichung beteiligte Funktion nur von einer einzelnen Variablen abhängt, sind ihre Ableitungen gewöhnliche Ableitungen, und die Differentialgleichung wird als gewöhnliche Differentialgleichung klassifiziert. Wenn andererseits die Funktion von mehreren unabhängigen Variablen abhängt, so dass ihre Ableitungen partielle Ableitungen sind, wird die Differentialgleichung als partielle Differentialgleichung klassifiziert. Das Folgende sind Beispiele für gewöhnliche Differentialgleichungen:
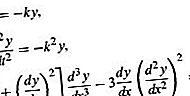
In diesen steht y für die Funktion und entweder t oder x ist die unabhängige Variable. Die Symbole k und m werden hier verwendet, um für bestimmte Konstanten zu stehen.
Unabhängig vom Typ wird eine Differentialgleichung als n-te Ordnung bezeichnet, wenn sie eine Ableitung der n-ten Ordnung, aber keine Ableitung einer höheren Ordnung als diese beinhaltet. Die Gleichung ist ein Beispiel einer partiellen Differentialgleichung zweiter Ordnung. Die Theorien der gewöhnlichen und partiellen Differentialgleichungen unterscheiden sich deutlich, weshalb die beiden Kategorien getrennt behandelt werden.
Anstelle einer einzelnen Differentialgleichung kann das Untersuchungsobjekt ein simultanes System solcher Gleichungen sein. Die Formulierung der Gesetze der Dynamik führt häufig zu solchen Systemen. In vielen Fällen kann eine einzelne Differentialgleichung der n-ten Ordnung vorteilhafterweise durch ein System von n simultanen Gleichungen ersetzt werden, von denen jede von der ersten Ordnung ist, so dass Techniken aus der linearen Algebra angewendet werden können.
Eine gewöhnliche Differentialgleichung, in der zum Beispiel die Funktion und die unabhängige Variable mit y und x bezeichnet sind, ist tatsächlich eine implizite Zusammenfassung der wesentlichen Eigenschaften von y als Funktion von x. Diese Eigenschaften wären vermutlich für die Analyse zugänglicher, wenn eine explizite Formel für y erstellt werden könnte. Eine solche Formel oder zumindest eine Gleichung in x und y (ohne Ableitungen), die aus der Differentialgleichung ableitbar ist, wird als Lösung der Differentialgleichung bezeichnet. Der Prozess des Ableitens einer Lösung aus der Gleichung durch Anwendung von Algebra und Kalkül wird als Lösen oder Integrieren der Gleichung bezeichnet. Es ist jedoch zu beachten, dass die Differentialgleichungen, die explizit gelöst werden können, nur eine kleine Minderheit bilden. Daher müssen die meisten Funktionen mit indirekten Methoden untersucht werden. Auch seine Existenz muss nachgewiesen werden, wenn keine Möglichkeit besteht, es zur Inspektion vorzulegen. In der Praxis werden Methoden aus der numerischen Analyse unter Einbeziehung von Computern eingesetzt, um nützliche Näherungslösungen zu erhalten.