Geometrie des Kegelschnittes

Kegelschnitt, auch als konischer, in der Geometrie, erzeugt jede Kurve, die durch den Schnitt einer Ebene und einer geraden kreisförmigen Kegel. Abhängig vom Winkel der Ebene relativ zum Kegel ist der Schnittpunkt ein Kreis, eine Ellipse, eine Hyperbel oder eine Parabel. Spezielle (entartete) Schnittfälle treten auf, wenn die Ebene nur durch den Scheitelpunkt (der einen einzelnen Punkt erzeugt) oder durch den Scheitelpunkt und einen anderen Punkt auf dem Kegel (der eine gerade Linie oder zwei sich kreuzende gerade Linien erzeugt) verläuft. Siehe die Abbildung.

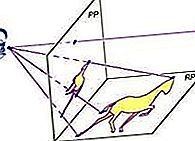
Projektive Geometrie: Projektive Kegelschnitte

Kegelschnitte können als ebene Abschnitte eines rechten Kreiskegels betrachtet werden (siehe Abbildung). Durch Betrachten

Die grundlegenden Beschreibungen, aber nicht die Namen der Kegelschnitte lassen sich auf Menaechmus (blühend um 350 v. Chr.) Zurückführen, einen Schüler sowohl von Platon als auch von Eudoxus von Cnidus. Apollonius von Perga (ca. 262–190 v. Chr.), Bekannt als „Großer Geometer“, gab den Kegelschnitten ihre Namen und definierte als erster die beiden Zweige der Hyperbel (die den Doppelkegel voraussetzen). Apollonius 'achtbändige Abhandlung über die Kegelschnitte, Conics, ist eines der größten wissenschaftlichen Werke der Antike.

Analytische Definition

Kegel können auch als ebene Kurven beschrieben werden, bei denen es sich um die Pfade (Loci) eines sich bewegenden Punkts handelt, so dass das Verhältnis seiner Entfernung von einem festen Punkt (dem Fokus) zur Entfernung von einer festen Linie (der Geraden) eine Konstante ist, die als Konstante bezeichnet wird die Exzentrizität der Kurve. Wenn die Exzentrizität Null ist, ist die Kurve ein Kreis; wenn gleich eins, eine Parabel; wenn weniger als eins, eine Ellipse; und wenn größer als eins, eine Hyperbel. Siehe die Abbildung.

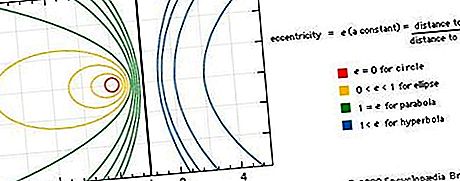
Jeder Kegelschnitt entspricht dem Graphen einer Polynomgleichung zweiten Grades der Form Ax ² + By ² + 2Cxy + 2Dx + 2Ey + F = 0, wobei x und y Variablen sind und A, B, C, D, E und F sind Koeffizienten, die vom jeweiligen Kegel abhängen. Durch eine geeignete Wahl der Koordinatenachsen kann die Gleichung für jeden Kegel auf eine von drei einfachen r-Formen reduziert werden: ^{x 2 / _{a 2} + y 2 / _{b 2} = 1, x 2 / _{a 2} - y 2 / _{b 2} = 1 oder y 2 = 2px, entsprechend einer Ellipse, einer Hyperbel bzw. einer Parabel. (Eine Ellipse mit a = b ist tatsächlich ein Kreis.) Die weit verbreitete Verwendung von Koordinatensystemen für die algebraische Analyse geometrischer Kurven stammt von René Descartes (1596–1650). Siehe Geschichte der Geometrie: Kartesische Geometrie.}

griechische Wurzeln

Die frühe Geschichte der Kegelschnitte ist mit dem Problem der „Verdoppelung des Würfels“ verbunden. Nach Eratosthenes von Cyrene (ca. 276–190 v. Chr.) Konsultierten die Einwohner von Delos das Orakel von Apollo, um Hilfe bei der Beendigung einer Pest zu erhalten (ca. 430 v. Chr.), Und wurden angewiesen, Apollo einen neuen Altar mit dem doppelten Volumen des alten Altars zu bauen und mit der gleichen kubischen Form. Verwirrt konsultierten die Delianer Platon, der erklärte: „Das Orakel bedeutete nicht, dass der Gott einen doppelt so großen Altar wollte, sondern dass er die Griechen für ihre Vernachlässigung der Mathematik und ihre Verachtung beschämen wollte, indem er ihnen die Aufgabe stellte für Geometrie. " Hippokrates von Chios (ca. 470–410 v. Chr.) Entdeckte erstmals, dass das „Delian-Problem“ darauf reduziert werden kann, zwei mittlere Proportionen zwischen a und 2a (die Volumina der jeweiligen Altäre) zu finden - das heißt, x und y so zu bestimmen, dass a: x = x: y = y: 2a. Dies entspricht der gleichzeitigen Lösung von zwei der Gleichungen x ² = ay, y ² = 2ax und xy = 2a ², die zwei Parabeln bzw. einer Hyperbel entsprechen. Später zeigte Archimedes (ca. 290–211 v. Chr.), Wie man mit Kegelschnitten eine Kugel in zwei Segmente mit einem bestimmten Verhältnis unterteilt.

Diokles (ca. 200 v. Chr.) Zeigten geometrisch, dass sich Strahlen - beispielsweise von der Sonne - parallel zur Achse eines Rotationsparaboloids (erzeugt durch Drehen einer Parabel um ihre Symmetrieachse) im Fokus treffen. Archimedes soll diese Eigenschaft genutzt haben, um feindliche Schiffe in Brand zu setzen. Die zentralen Eigenschaften der Ellipse wurden von Anthemius von Tralles, einem der Architekten der Kathedrale Hagia Sophia in Konstantinopel (fertiggestellt 537 n. Chr.), Zitiert, um sicherzustellen, dass ein Altar den ganzen Tag über vom Sonnenlicht beleuchtet werden kann.