Eudoxus von Cnidus (ca. 400–350 v. Chr.) Geht die Ehre, als erster zu zeigen, dass die Fläche eines Kreises proportional zum Quadrat seines Radius ist. In der heutigen algebraischen Notation wird diese Proportionalität durch die bekannte Formel A = πr 2 ausgedrückt. Die Proportionalitätskonstante π ist trotz ihrer Vertrautheit höchst mysteriös, und das Bestreben, sie zu verstehen und ihren genauen Wert zu finden, beschäftigt die Mathematiker seit Tausenden von Jahren. Ein Jahrhundert nach Eudoxus fand Archimedes die erste gute Annäherung an π: 3 10 / 71 <π <3 1 / 7. Dies erreichte er durch Annäherung eines Kreises mit einem 96-seitigen Polygon (siehe Animation). Noch bessere Annäherungen wurden gefunden, indem Polygone mit mehr Seiten verwendet wurden, aber diese dienten nur dazu, das Rätsel zu vertiefen, da kein genauer Wert erreicht werden konnte und kein Muster in der Folge von Annäherungen beobachtet werden konnte.
Eine erstaunliche Lösung des Geheimnisses wurde von indischem Mathematiker etwa 1500 ce entdeckt: π kann durch die unendliche dargestellt werden, aber verblüffend einfache, Serie π / 4 = 1 - 1 / 3 + 1 / 5 - 1 / 7 + ⋯.They entdeckt dies als Sonderfall der Serie für die inverse Tangensfunktion: tan -1 (x) = x - x 3 / 3 + x 5 / 5 - x 7 / 7 + ⋯.
Die einzelnen Entdecker dieser Ergebnisse sind nicht sicher bekannt; Einige Gelehrte schreiben sie Nilakantha Somayaji zu, andere Madhava. Die indischen Beweise ähneln strukturell den später in Europa von James Gregory, Gottfried Wilhelm Leibniz und Jakob Bernoulli entdeckten Beweisen. Der Hauptunterschied besteht darin, dass die Indianer, wo die Europäer den Vorteil des Grundsatzes der Analysis hatten, Grenzen von Summen der Form finden mussten
Vor Gregors Wiederentdeckung der inversen Tangentenreihe um 1670 wurden in Europa andere Formeln für π entdeckt. Im Jahr 1655 entdeckte John Wallis das unendliche Produkt π / 4 = 2 / 3 ∙ 4 / 3 ∙ 4 / 5 ∙ 6 / 5 ∙ 6 / 7 ⋯, und sein Kollege William Brouncker verwandelte diese in den unendlichen Kettenbruch
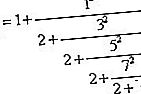
Schließlich in Leonhard Eulersche Einführung in die Analyse des Unendlichen (1748), die Reihe π / 4 = 1 - 1 / 3 + 1 / 5 - 1 / 7 + ⋯ in Brouncker des Kettenbruch transformiert, was zeigt, daß alle drei Formeln sind in manche spüren das auch.
Brounckers unendliche fortgesetzte Fraktion ist besonders bedeutsam, weil sie darauf hindeutet, dass π keine gewöhnliche Fraktion ist - mit anderen Worten, dass π irrational ist. Genau diese Idee wurde im ersten Beweis verwendet, dass π irrational ist, den Johann Lambert 1767 gegeben hat.













