Quadratur der Lune

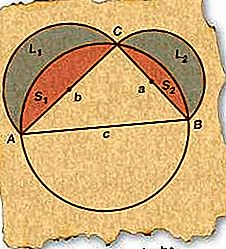
Hippokrates von Chios (vlnr 460 v. Chr.) Zeigte, dass die mondförmigen Bereiche zwischen Kreisbögen, die als Lunes bezeichnet werden, genau als geradlinige Fläche oder Quadratur ausgedrückt werden können. Im folgenden einfachen Fall haben zwei um die Seiten eines rechtwinkligen Dreiecks entwickelte Lunes eine kombinierte Fläche, die der des Dreiecks entspricht.

1. Zeichnen Sie beginnend mit dem rechten ΔABC einen Kreis, dessen Durchmesser mit AB (Seite c), der Hypotenuse, übereinstimmt. Da jedes rechtwinklige Dreieck, dessen Hypotenuse mit dem Durchmesser eines Kreises gezeichnet wurde, in den Kreis eingeschrieben werden muss, muss sich C auf dem Kreis befinden.

2. Zeichnen Sie Halbkreise mit den Durchmessern AC (Seite b) und BC (Seite a) wie in der Abbildung.

3. Beschriften Sie die resultierenden Lunes L ₁ und L ₂ und die resultierenden Segmente S ₁ und S ₂, wie in der Abbildung gezeigt.

4. Nun muss die Summe der Lunes (L ₁ und L ₂) gleich der Summe der Halbkreise (L ₁ + S ₁ und L ₂ + S ₂) sein, die sie enthalten, abzüglich der beiden Segmente (S ₁ und S ₂). Somit ist L ₁ + L ₂ = ^π / ₂ (^b / ₂) ² - S ₁ + ^π / ₂ (^a / ₂) ² - S ₂ (da die Fläche eines Kreises das π-fache des Quadrats des Radius beträgt).

5. Die Summe der Segmente (S ₁ und S ₂) entspricht der Fläche des Halbkreises basierend auf AB minus der Fläche des Dreiecks. So, S ₁ + S ₂ = ^π / ₂ (^c / ₂) ² - ΔABC.

6. Einsetzen des Ausdrucks in Schritt 5 in Schritt 4 und Ausklammern gemeinsamer Terme, L ₁ + L ₂ = ^π / ₈ (a ² + b ² - c ²) + ΔABC.

7. Da ∠ACB = 90 ° ist, ist nach dem Satz von Pythagoras a ² + b ² - c ² = 0. Somit ist L ₁ + L ₂ = & Dgr; ABC.

   Hippokrates schaffte es, mehrere Arten von Lunes zu quadrieren, einige auf Bögen, die größer und kleiner als Halbkreise waren, und er deutete an, obwohl er vielleicht nicht geglaubt hatte, dass seine Methode einen ganzen Kreis quadrieren könnte. Am Ende des klassischen Zeitalters erwähnte Boethius (ca. 470–524 n. Chr.), Dessen lateinische Übersetzungen von Euklidschnipsel das Licht der Geometrie ein halbes Jahrtausend lang flackern ließen, dass jemand die Quadratur des Kreises erreicht hatte. Ob das unbekannte Genie Lunes oder eine andere Methode verwendete, ist nicht bekannt, da Boethius aus Platzgründen die Demonstration nicht gab. Er übertrug damit die Herausforderung der Quadratur des Kreises zusammen mit Fragmenten der Geometrie, die offensichtlich nützlich für die Durchführung waren. Die Europäer blieben bis weit in die Aufklärung hinein bei der unglücklichen Aufgabe. Schließlich weigerte sich die Pariser Akademie der Wissenschaften, die es satt hatte, die Irrtümer in den vielen ihr vorgelegten Lösungen zu erkennen, 1775, nichts weiter mit Kreisquadratern zu tun zu haben.